Numerical Test Tip 3 - Remember to take away ‘overlaps’ and/or add in for ‘overhangs’
Trickier questions in numerical reasoning questions, like those that ask you to calculate a frame or a tablecloth may actually ask you to add in calculations (one of each side of the table) in order to get to the correct answer. There are other questions where you might need to minus the overlap. Let’s see one now.
Question 3
A rectangular lawn 55 metres by 35 meters has two roads, each 4 metres wide running in the middle of it, one parallel to one side of the lawn while the other parallel to breadth. The cost of gravelling the roads at $0.75 per square metres is:
A: $422 B: $511 C:$420 D: $258 E: $32
Solution:
Step 1: Illustrate the concept on paper
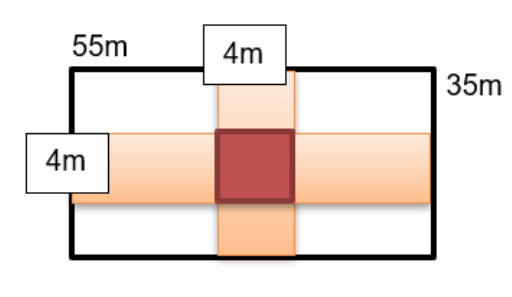
Step 2: Calculate the total square metres of the road
Since the roads intersect at the center we have to calculate that square space in the middle only once:
4x35 + 4x55 – 4x4 = 140 + 220 – 16 = 344 sq.m.
Step 3: Calculate the cost of gravelling
344 x 0.75 = $258
The correct answer is D.
Note that if we hadn’t illustrated the concept on paper, it would have been really easy to miss out on a little, yet essential detail – the fact that roads intersect.
And this means wasted time, lost scores, and lost opportunities.
Numerical Test Tip 4 - Know which operators to use with certain words
One of the trickiest things with numerical reasoning (especially if English is not your native language) is bridging the connection between the worded question and deciding on which mathematical operators to use when doing calculations.
This is because it’s not just about calculating, it’s about reading comprehension - understanding the question and knowing what’s asked of you.
Here’s a cheat sheet. When a question has the word:
- Of - it generally implies multiplication.
- And - it generally implies addition.
- Parts - it generally implies division, fractions and ratios.
- Within - it generally implies fractions.
- Total - it generally implies addition.
- Difference - it generally implies subtraction.
Now, let’s see this in action through a sample practice question.
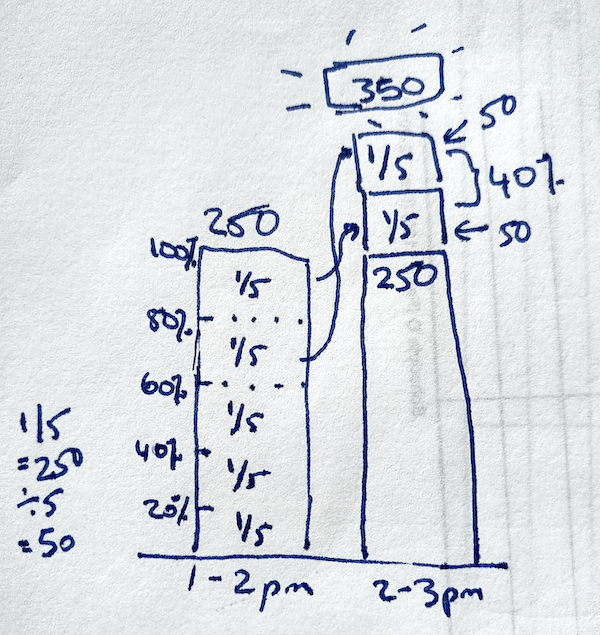
Question 4
A certain recipe of chocolate milk shake contains 2 parts of milk and 3 parts of chocolates per litre. In order to prepare 350 litres of the same recipe, how many litres of milk is required?
A: 150 B: 280 C: 210 D: 140 E: 235
Solution:
There are a lot of words being used here. Here the words “part” mean fractions of a litre, so 2 parts and (+) 3 parts is 5 parts. The word “of” here doesn’t mean you have to multiply but that the parts belong to certain groups of ingredients e.g. milk and chocolate.
Check out the video solution here:
Numerical Test Tip 5 - Know the whole and its parts
It’s very easy to get confused with the different types of ways that parts of a whole are presented. Here are rules to remember:
- Ratios - when you have something that looks like 2:2:4, this means in total, you have 8 parts (2+2+4) of 1 whole but that whole is split unevenly between 3 people. 2 people (Person A & B) get 2 parts each and then Person C gets double of what Person A or B has.
- Fractions - this represents one part of a whole and can be expressed in multiple ways. If that part is larger than 1 whole, you’ll see something like this 1.5 of 3 / 2.
- Wholes - for percentages, the whole is expressed at 100% but it doesn’t mean that it is 100. It could be 5 cats in a basket (100%) and if 40% are sold, that means 2 cats have been sold.
Onwards now… to the practice question.
Question 5
Jack and John share the fish caught in the ratio of 3:5. If Jack caught 180 fish, how many did John catch?
A: 300 B: 280 C: 230 D: 180 E: None of the above
Solution:
Step 1: Set up the calculation formula through reasoning
3 parts and 5 parts means that in total you have 8 parts. Jack has 3 of the 8 parts, John has 5 of the 8 parts. Jack has 180 which means that each of the 8 parts is worth 60 because he has 3 of them (180 divided by 3).
Step 2: Reason to the answer
John has 5 of the 8 parts so that’s 300 (because 5 x 60), Option A. Simple right?
There are other ways you could have set up this solution. One way is this:
3/8 = 180
5⁄8 = f
f = (5⁄8 x 180 )/(3⁄8) = 900/3 = 300
The correct answer is A.
But... this is longer and harder to do. The easier way is to reason and to reason well with parts, you need to understand the whole and its parts.
Practice Online to Ace Your Job or School Aptitude Test
We’ve put in hundreds of hours designing efficient test prep tools to help you get real results. See available test preparation to help you ace your exam now.